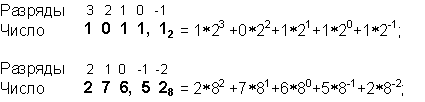
| Система счисления — это способ записи чисел с помощью заданного набора специальных знаков (цифр). |
Существуют позиционные и непозиционные системы счисления.
В непозиционных системах вес цифры (т.е. тот вклад, который она вносит в значение числа) не зависит от ее позиции в записи числа. Так, в римской системе счисления в числе ХХХII (тридцать два) вес цифры Х в любой позиции равен просто десяти.
В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число. Например, в числе 757,7 первая семерка означает 7 сотен, вторая – 7 единиц, а третья – 7 десятых долей единицы.
Сама же запись числа 757,7 означает сокращенную запись выражения
700 + 50 + 7 + 0,7 = 7•102 + 5•101 + 7•100 + 7•10-1 = 757,7.
Любая позиционная система счисления характеризуется своим основанием.
| Основание позиционной системы счисления — это количество различных знаков или символов, используемых для изображения цифр в данной системе. |
За основание системы можно принять любое натуральное число — два, три, четыре и т.д. Следовательно, возможно бесчисленное множество позиционных систем: двоичная, троичная, четверичная и т.д. Запись чисел в каждой из систем счисления с основанием q означает сокращенную запись выражения
an-1 qn-1 + an-2 qn-2+ ... + a1 q1 + a0 q0 + a-1 q-1 + ... + a-m q-m,
где ai – цифры системы счисления; n и m – число целых и дробных разрядов, соответственно.
Например:
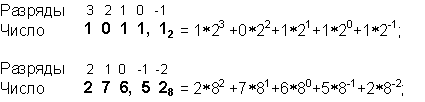
В каждой системе счисления цифры упорядочены в соответствии с их значениями: 1 больше 0, 2 больше 1 и т.д.
| Продвижением цифры называют замену её следующей по величине. |
Продвинуть цифру 1 значит заменить её на 2, продвинуть цифру 2 значит заменить её на 3 и т.д. Продвижение старшей цифры (например, цифры 9 в десятичной системе) означает замену её на 0. В двоичной системе, использующей только две цифры – 0 и 1, продвижение 0 означает замену его на 1, а продвижение 1 – замену её на 0.
Целые числа в любой системе счисления порождаются с помощью Правила счета [44]:
| Для образования целого числа, следующего за любым данным целым числом, нужно продвинуть самую правую цифру числа; если какая-либо цифра после продвижения стала нулем, то нужно продвинуть цифру, стоящую слева от неё. |
Применяя это правило, запишем первые десять целых чисел
Кроме десятичной широко используются системы с основанием, являющимся целой степенью числа 2, а именно:
Полезно запомнить запись в этих системах счисления первых двух десятков целых чисел:
|
|
Из всех систем счисления особенно проста и поэтому интересна для технической реализации в компьютерах двоичная система счисления.
Люди предпочитают десятичную систему, вероятно, потому, что с древних времен считали по пальцам, а пальцев у людей по десять на руках и ногах. Не всегда и не везде люди пользуются десятичной системой счисления. В Китае, например, долгое время пользовались пятеричной системой счисления.
А компьютеры используют двоичную систему потому, что она имеет ряд преимуществ перед другими системами:
Недостаток двоичной системы — быстрый рост числа разрядов, необходимых для записи чисел.
Двоичная система, удобная для компьютеров, для человека неудобна из-за ее громоздкости и непривычной записи.
Перевод чисел из десятичной системы в двоичную и наоборот выполняет машина. Однако, чтобы профессионально использовать компьютер, следует научиться понимать слово машины. Для этого и разработаны восьмеричная и шестнадцатеричная системы.
Числа в этих системах читаются почти так же легко, как десятичные, требуют соответственно в три (восьмеричная) и в четыре (шестнадцатеричная) раза меньше разрядов, чем в двоичной системе (ведь числа 8 и 16 – соответственно, третья и четвертая степени числа 2).
| Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему очень прост: достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр). |
Например:

| Чтобы перевести число из двоичной системы в восьмеричную или шестнадцатеричную, его нужно разбить влево и вправо от запятой на триады (для восьмеричной) или тетрады (для шестнадцатеричной) и каждую такую группу заменить соответ-ствующей восьмеричной (шестнадцатеричной) цифрой. |
Например,
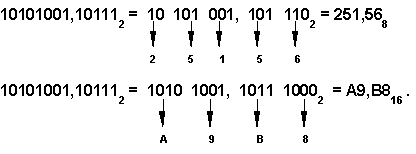
| При переводе целого десятичного числа в систему с основанием q его необходимо последовательно делить на q до тех пор, пока не останется остаток, меньший или равный q–1. Число в системе с основанием q записывается как последо-вательность остатков от деления, записанных в обратном порядке, начиная с последнего. |
Пример: Перевести число 75 из десятичной системы в двоичную,
восьмеричную и шестнадцатеричную:
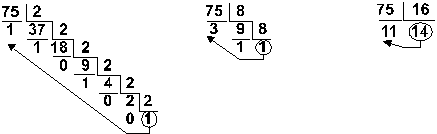
Ответ: 7510 = 1 001 0112 = 1138 = 4B16.
| Пpи переводе правильной десятичной дpоби в систему счисления с основанием q необходимо сначала саму дробь, а затем дробные части всех последующих произведений последовательно умножать на q, отделяя после каждого умножения целую часть пpоизведения. Число в новой системе счисления записывается как последовательность полученных целых частей пpоизведения. |
Умножение пpоизводится до тех поp, пока дpобная часть пpоизведения не станет pавной нулю. Это значит, что сделан точный пеpевод. В пpотивном случае пеpевод осуществляется до заданной точности. Достаточно того количества цифp в pезультате, котоpое поместится в ячейку.
Пример: Перевести число 0,35 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:
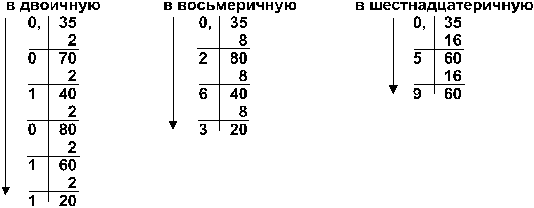
Ответ: 0,3510 = 0,010112 = 0,2638 = 0,5916 .
| При переводе числа из двоичной (восьмеричной, шестнадцатеричной) системы в десятичную надо это число представить в виде суммы степеней основания его системы счисления. |
Примеpы:
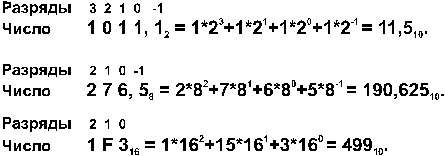
Рассмотрим только те системы счисления, которые применяются в компьютерах — десятичную, двоичную, восьмеричную и шестнадцатеричную.
Для определенности возьмем произвольное десятичное число, например 46, и для него выполним все возможные последовательные переводы из одной системы счисления в другую.
Порядок переводов определим в соответствии с рисунком:
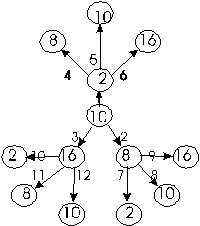
На этом рисунке использованы следующие обозначения:
Например: ![]() означает перевод из двоичной системы в шестнадцатеричную, имеющий в таблице
порядковый номер 6.
означает перевод из двоичной системы в шестнадцатеричную, имеющий в таблице
порядковый номер 6.


Рассмотрим основные арифметические операции: сложение, вычитание, умножение и деление. Правила выполнения этих операций в десятичной системе хорошо известны — это сложение, вычитание, умножение столбиком и деление углом. Эти правила применимы и ко всем другим позиционным системам счисления. Только таблицами сложения и умножения надо пользоваться особыми для каждой системы.
Таблицы сложения легко составить, используя Правило Счета.
|
Сложение в двоичной системе
|
Сложение в восьмеричной системе
|
Сложение в шестнадцатиричной системе

При сложении цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево.
Пример 1. Сложим числа 15 и 6 в различных системах счисления.
![]()
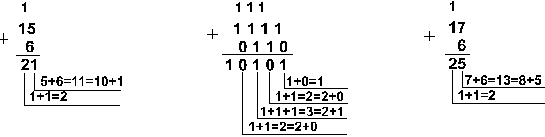
|
Шестнадцатеричная: F16+616
|
Ответ: 15+6 = 2110 = 101012 = 258 = 1516. Проверка. Преобразуем полученные суммы к десятичному
виду: |
Пример 2. Сложим числа 15, 7 и 3.
![]()
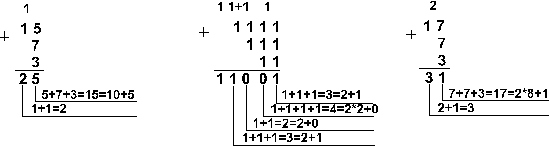
|
Шестнадцатеричная: F16+716+316
|
Ответ: 5+7+3 = 2510 = 110012 = 318 = 1916. Проверка:
|
Пример 3. Сложим числа 141,5 и 59,75.
![]()
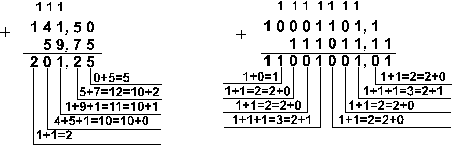
![]()
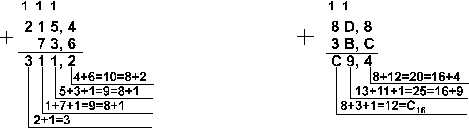
Ответ: 141,5 + 59,75 = 201,2510 = 11001001,012 = 311,28 = C9,416
Проверка. Преобразуем полученные суммы к десятичному виду:
11001001,012 = 27 + 26 + 23 +
20 + 2-2 = 201,25
311,28 = 3*82
+ 1•81 + 1*80 + 2*8-1 = 201,25
C9,416 = 12*161 + 9*160 + 4*16-1
= 201,25
Пример 4. Вычтем единицу из чисел 102, 108 и 1016
![]()
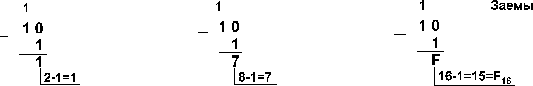
Пример 5. Вычтем единицу из чисел 1002, 1008 и 10016.
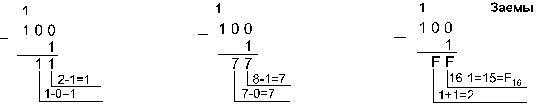
![]()
Пример 6. Вычтем число 59,75 из числа 201,25.
![]()
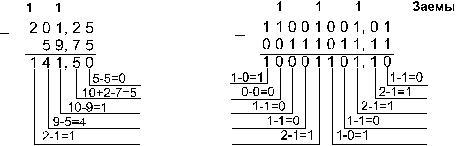
![]()

Ответ: 201,2510 – 59,7510 = 141,510 = 10001101,12 = 215,48 = 8D,816.
Проверка. Преобразуем полученные разности к десятичному виду:
10001101,12 = 27 + 23 + 22 +
20 + 2–1 = 141,5;
215,48 = 2*82
+ 1*81 + 5*80 + 4*8–1 = 141,5;
8D,816 = 8*161 + D*160 + 8*16–1
= 141,5.
Выполняя умножение многозначных чисел в различных позиционных системах
счисления, можно использовать обычный алгоритм перемножения чисел в столбик, но
при этом результаты перемножения и сложения однозначных чисел необходимо
заимствовать из соответствующих рассматриваемой системе таблиц умножения и
сложения.
|
Умножение в двоичной системе
|
Умножение в восьмеричной системе
|
Ввиду чрезвычайной простоты таблицы умножения в двоичной системе, умножение сводится лишь к сдвигам множимого и сложениям.
Пример 7. Перемножим числа 5 и 6.
![]()
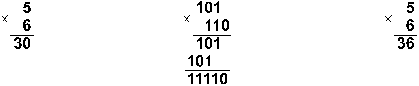
Ответ: 5*6 = 3010 = 111102 = 368.
Проверка. Преобразуем полученные произведения к десятичному виду:
111102 = 24 + 23 + 22 +
21 = 30;
368 = 3•81 + 6•80 = 30.
Пример 8. Перемножим числа 115 и 51.
![]()
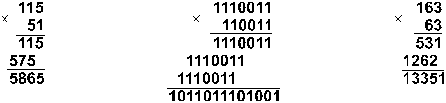
Ответ: 115*51 = 586510 = 10110111010012 = 133518.
Проверка. Преобразуем полученные произведения к десятичному виду:
10110111010012 = 212 + 210 + 29
+ 27 + 26 + 25 + 23 + 20
= 5865;
133518 = 1*84 + 3*83 +
3*82 + 5*81 + 1*80 = 5865.
Деление в любой позиционной системе счисления производится по тем же правилам, как и деление углом в десятичной системе. В двоичной системе деление выполняется особенно просто, ведь очередная цифра частного может быть только нулем или единицей.
Пример 9. Разделим число 30 на число 6.
![]()
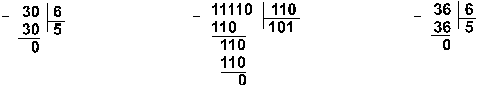
Ответ: 30 : 6 = 510 = 1012 = 58.
Пример 10. Разделим число 5865 на число 115.
![]()
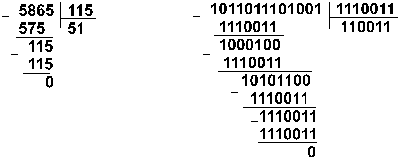
Восьмеричная: 133518 :1638
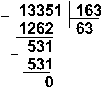
Ответ: 5865 : 115 = 5110 = 1100112 = 638.
Проверка. Преобразуем полученные частные к десятичному виду:
1100112 = 25 + 24 + 21 +
20 = 51; 638 = 6*81 + 3*80 = 51.
Пример 11. Разделим число 35 на число 14.

![]()
Восьмеричная: 438 : 168
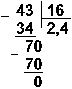
Ответ: 35 : 14 = 2,510 = 10,12 = 2,48.
Проверка. Преобразуем полученные частные к десятичному виду:
10,12 = 21 + 2 -1 = 2,5;
2,48 = 2*80 + 4*8-1 = 2,5.
Целые числа могут представляться в компьютере со знаком или без знака.
Целые числа без знака обычно занимают в памяти один или два байта и принимают в однобайтовом формате значения от 000000002 до 111111112 , а в двубайтовом формате — от 00000000 000000002 до 11111111 111111112.
| Формат числа в байтах | Диапазон | |
| Запись с порядком | Обычная запись | |
| 1 | 0 ... 28–1 | 0 ... 255 |
| 2 | 0 ... 216–1 | 0 ... 65535 |
Примеры:
а) число 7210 = 10010002 в однобайтовом формате:
![]()
б) это же число в двубайтовом формате:
![]()
в) число 65535 в двубайтовом формате:
![]()
Целые числа со знаком обычно занимают в памяти компьютера один, два или четыре байта, при этом самый левый (старший) разряд содержит информацию о знаке числа. Знак “плюс” кодируется нулем, а “минус” — единицей.
| Формат числа в байтах | Диапазон | |
| Запись с порядком | Обычная запись | |
| 1 | –27 ... 27–1 | –128 ... 127 |
| 2 | –215 ... 215–1 | –32768 ... 32767 |
| 4 | –231 ... 231–1 | –2147483648 ... 2147483647 |
Рассмотрим особенности записи целых чисел со знаком на примере однобайтового формата, при котором для знака отводится один разряд, а для цифр абсолютной величины – семь разрядов.
| В компьютерной технике применяются три формы записи (кодирования) целых чисел со знаком: прямой код, обратный код, дополнительный код. |
Последние две формы применяются особенно широко, так как позволяют упростить конструкцию арифметико-логического устройства компьютера путем замены разнообразных арифметических операций операцией cложения.
Положительные числа в прямом, обратном и дополнительном кодах изображаются одинаково — двоичными кодами с цифрой 0 в знаковом разряде. Например:

Отрицательные числа в прямом, обратном и дополнительном кодах имеют разное изображение.
1. Прямой код. В знаковый разряд помещается цифра 1, а в разряды цифровой части числа — двоичный код его абсолютной величины. Например:
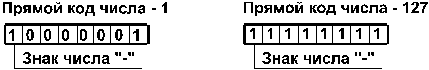
2. Обратный код. Получается инвертированием всех цифр двоичного кода абсолютной величины числа, включая разряд знака: нули заменяются единицами, а единицы — нулями. Например:

3. Дополнительный код. Получается образованием обратного кода с последующим прибавлением единицы к его младшему разряду. Например:
| Обычно отрицательные десятичные числа при вводе в машину автоматически преобразуются в обратный или дополнительный двоичный код и в таком виде хранятся, перемещаются и участвуют в операциях. При выводе таких чисел из машины происходит обратное преобразование в отрицательные десятичные числа. |
| В большинстве компьютеров операция вычитания не используется. Вместо нее производится сложение уменьшаемого с обратным или дополнительным кодом вычитаемого. Это позволяет существенно упростить конструкцию АЛУ. |
При сложении обратных кодов чисел А и В имеют место четыре основных и два особых случая:
1. А и В положительные. При суммировании складываются все разряды, включая разряд знака. Так как знаковые разряды положительных слагаемых равны нулю, разряд знака суммы тоже равен нулю. Например:

Получен правильный результат.
2. А положительное, B отрицательное и по абсолютной величине больше, чем А. Например:
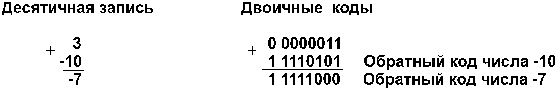
Получен правильный результат в обратном коде. При переводе в прямой код биты цифровой части результата инвертируются: 1 0000111 = –710.
3. А положительное, B отрицательное и по абсолютной величине меньше, чем А. Например:

Компьютер исправляет полученный первоначально неправильный результат (6 вместо 7) переносом единицы из знакового разряда в младший разряд суммы.
4. А и В отрицательные. Например:

Полученный первоначально неправильный результат (обратный код числа –1110 вместо обратного кода числа –1010) компьютер исправляет переносом единицы из знакового разряда в младший разряд суммы.
При переводе результата в прямой код биты цифровой части числа инвертируются: 1 0001010 = –1010.
При сложении может возникнуть ситуация, когда старшие разряды результата операции не помещаются в отведенной для него области памяти. Такая ситуация называется переполнением разрядной сетки формата числа. Для обнаружения переполнения и оповещения о возникшей ошибке в компьютере используются специальные средства. Ниже приведены два возможных случая переполнения.
5. А и В положительные, сумма А+В больше, либо равна 2n–1, где n – количество разрядов формата чисел (для однобайтового формата n=8, 2n–1 = 27 = 128). Например:
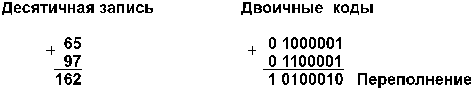
Семи разрядов цифровой части числового формата недостаточно для размещения восьмиразрядной суммы (16210 = 101000102), поэтому старший разряд суммы оказывается в знаковом разряде. Это вызывает несовпадение знака суммы и знаков слагаемых, что является свидетельством переполнения разрядной сетки.
6. А и В отрицательные, сумма абсолютных величин А и В больше, либо равна 2n–1. Например:

Здесь знак суммы тоже не совпадает со знаками слагаемых, что свидетельствует о переполнении разрядной сетки.
Все эти случаи имеют место и при сложении дополнительных кодов чисел:
1. А и В положительные. Здесь нет отличий от случая 1, рассмотренного для обратного кода.
2. А положительное, B отрицательное и по абсолютной величине больше, чем А. Например:

Получен правильный результат в дополнительном коде. При переводе в прямой код биты цифровой части результата инвертируются и к младшему разряду прибавляется единица: 1 0000110 + 1 = 1 0000111 = –710.
3. А положительное, B отрицательное и по абсолютной величине меньше, чем А. Например:

Получен правильный результат. Единицу переноса из знакового разряда компьютер отбрасывает.
4. А и В отрицательные. Например:

Получен правильный результат в дополнительном коде. Единицу переноса из знакового разряда компьютер отбрасывает.
Случаи переполнения для дополнительных кодов рассматриваются по аналогии со случаями 5 и 6 для обратных кодов.
Сравнение рассмотренных форм кодирования целых чисел со знаком показывает:
Во многих компьютерах умножение производится как последовательность сложений и сдвигов. Для этого в АЛУ имеется регистр, называемый накапливающим сумматором, который до начала выполнения операции содержит число ноль. В процессе выполнения операции в нем поочередно размещаются множимое и результаты промежуточных сложений, а по завершении операции — окончательный результат.
Другой регистр АЛУ, участвующий в выполнении этой операции, вначале содержит множитель. Затем по мере выполнения сложений содержащееся в нем число уменьшается, пока не достигнет нулевого значения.
Для иллюстрации умножим 1100112 на 1011012.

Деление для компьютера является трудной операцией. Обычно оно реализуется путем многократного прибавления к делимому дополнительного кода делителя.
| Вещественными числами (в отличие от целых) в компьютерной технике называются числа, имеющие дробную часть. |
При их написании вместо запятой принято писать точку. Так, например, число 5 — целое, а числа 5.1 и 5.0 — вещественные.
Для удобства отображения чисел, принимающих значения из достаточно широкого диапазона (то есть, как очень маленьких, так и очень больших), используется форма записи чисел с порядком основания системы счисления. Например, десятичное число 1.25 можно в этой форме представить так:
или так:
| Любое число N в системе счисления с основанием q можно записать в виде N = M * qp, где M называется мантиссой числа, а p — порядком. Такой способ записи чисел называется представлением с плавающей точкой. |
Если “плавающая” точка расположена в мантиссе перед первой значащей цифрой, то при фиксированном количестве разрядов, отведённых под мантиссу, обеспечивается запись максимального количества значащих цифр числа, то есть максимальная точность представления числа в машине. Из этого следует:
| Мантисса должна быть правильной дробью, первая цифра которой отлична от нуля: M из [0.1, 1). |
Такое, наиболее выгодное для компьютера, представление вещественных чисел называется нормализованным.
Мантиссу и порядок q-ичного числа принято записывать в системе с основанием q, а само основание — в десятичной системе.
Примеры нормализованного представления:
Десятичная система Двоичная система
753.15 = 0.75315*103; -101.01 = -0.10101*211 (порядок 112 = 310)
-0.000034 = -0.34*10-4; -0.000011 = 0.11*2-100 (порядок -1002 = -410)
Вещественные числа в компьютерах различных типов записываются по-разному. При этом компьютер обычно предоставляет программисту возможность выбора из нескольких числовых форматов наиболее подходящего для конкретной задачи — с использованием четырех, шести, восьми или десяти байтов.
В качестве примера приведем характеристики форматов вещественных чисел,
используемых IBM-совместимыми персональными компьютерами:
| Форматы вещественных чисел | Размер в байтах | Примерный диапазон абсолютных значений | Количество значащих десятичных цифр |
| Одинарный | 4 | 10–45 … 1038 | 7 или 8 |
| Вещественный | 6 | 10–39 … 1038 | 11 или 12 |
| Двойной | 8 | 10–324 … 10308 | 15 или 16 |
| Расширенный | 10 | 10–4932 … 104932 | 19 или 20 |
Из этой таблицы видно, что форма представления чисел с плавающей точкой позволяет записывать числа с высокой точностью и из весьма широкого диапазона.
При хранении числа с плавающей точкой отводятся разряды для мантиссы, порядка, знака числа и знака порядка:
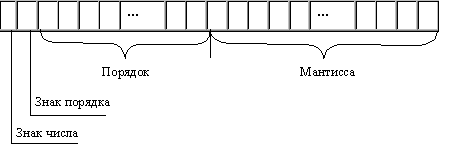
|
· Чем больше разрядов отводится под запись мантиссы, тем выше точность представления числа. · Чем больше разрядов занимает порядок, тем шире диапазон от наименьшего отличного от нуля числа до наибольшего числа, представимого в машине при заданном формате. |
Покажем на примерах, как записываются некоторые числа в нормализованном виде в четырехбайтовом формате с семью разрядами для записи порядка.
1. Число 6.2510 = 110.012 = 0,11001•211 :
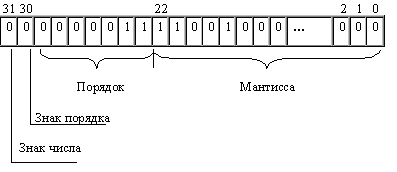
2. Число –0.12510 = –0.0012 = –0.1*2–10 (отрицательный порядок записан в дополнительном коде):
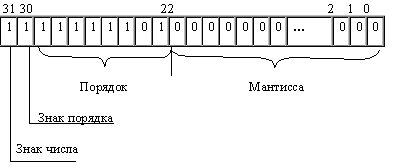
К началу выполнения арифметического действия операнды операции помещаются в соответствующие регистры АЛУ.
При сложении и вычитании сначала производится подготовительная операция, называемая выравниванием порядков.
| В процессе выравнивания порядков мантисса числа с меньшим порядком сдвигается в своем регистре вправо на количество разрядов, равное разности порядков операндов. После каждого сдвига порядок увеличивается на единицу. |
В результате выравнивания порядков одноименные разряды чисел оказываются расположенными в соответствующих разрядах обоих регистров, после чего мантиссы складываются или вычитаются.
В случае необходимости полученный результат нормализуется путем сдвига мантиссы результата влево. После каждого сдвига влево порядок результата уменьшается на единицу.
Пример 1. Сложить двоичные нормализованные числа 0.10111•2–1 и 0.11011*210. Разность порядков слагаемых здесь равна трем, поэтому перед сложением мантисса первого числа сдвигается на три разряда вправо:
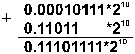
Пример 2. Выполнить вычитание двоичных нормализованных чисел 0.10101*210 и 0.11101*21. Разность порядков уменьшаемого и вычитаемого здесь равна единице, поэтому перед вычитанием мантисса второго числа сдвигается на один разряд вправо:
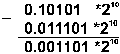
Результат получился не нормализованным, поэтому его мантисса сдвигается влево на два разряда с соответствующим уменьшением порядка на две единицы: 0.1101*20.
| При умножении двух нормализованных чисел их порядки складываются, а мантиссы перемножаются. |
Пример 3. Выполнить умножение двоичных нормализованных чисел:
| При делении двух нормализованных чисел из порядка делимого вычитается порядок делителя, а мантисса делимого делится на мантиссу делителя. Затем в случае необходимости полученный результат нормализуется. |
Пример 4. Выполнить деление двоичных нормализованных чисел:
Использование представления чисел с плавающей точкой существенно усложняет схему арифметико-логического устройства.
4.1. Используя Правило Счета, запишите первые 20 целых чисел в десятичной, двоичной, троичной, пятеричной и восьмеричной системах счисления.
4.2. Какие целые числа следуют за числами:
| а) 12; | е) 18; | п) F16; |
| б) 1012; | ж) 78; | м) 1F16; |
| в) 1112; | з) 378; | н) FF16; |
| г) 11112; | и) 1778; | о) 9AF916; |
| д) 1010112; | к) 77778; | п) CDEF16 ? |
4.3. Какие целые числа предшествуют числам:
| а) 102; | е) 108; | л) 1016; |
| б) 10102; | ж) 208; | м)2016; |
| в) 10002; | з) 1008; | н) 10016; |
| г) 100002; | и) 1108; | о) A1016; |
| д) 101002; | к) 10008; | п) 100016 ? |
4.4. Какой цифрой заканчивается четное двоичное число? Какой цифрой заканчивается нечетное двоичное число? Какими цифрами может заканчиваться четное троичное число?
4.5. Какое наибольшее десятичное число можно записать тремя цифрами:
4.6. В какой системе счисления 21 + 24 = 100?
4.7. В какой системе счисления справедливо следующее:
4.8. Десятичное число 59 эквивалентно числу 214 в некоторой другой системе счисления. Найдите основание этой системы.
4.9. Переведите числа в десятичную систему, а затем проверьте
результаты, выполнив обратные переводы:
| а) 10110112; | е) 5178; | л) 1F16; |
| б) 101101112; | ж) 10108; | м) ABC16; |
| в) 0111000012; | з) 12348; | н) 101016; |
| г) 0,10001102; | и) 0,348; | о) 0,А416; |
| д) 110100,112; | к) 123,418; | п) 1DE,C816. |
4.10. Переведите числа из десятичной системы в двоичную, восьмеричную и шестнадцатеричную, а затем проверьте результаты, выполнив обратные переводы:
а) 12510; б) 22910; в) 8810; г) 37,2510; д) 206,12510.
4.11. Переведите числа из двоичной системы в восьмеричную и
шестнадцатеричную, а затем проверьте результаты, выполнив обратные переводы:
| а) 1001111110111,01112; | г) 1011110011100,112; |
| б) 1110101011,10111012; | д) 10111,11111011112; |
| в) 10111001,1011001112; | е) 1100010101,110012. |
4.12. Переведите в двоичную и восьмеричную системы шестнадцатеричные числа:
а) 2СE16; б) 9F4016; в) ABCDE16; г) 1010,10116; д) 1ABC,9D16.
4.13. Выпишите целые числа:
4.14. Для десятичных чисел 47 и 79 выполните цепочку переводов из одной системы счисления в другую:
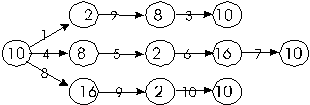
4.15. Составьте таблицы сложения однозначных чисел в троичной и пятеричной системах счисления.
4.16. Составьте таблицы умножения однозначных чисел в троичной и пятеричной системах счисления.
4.17. Сложите числа, а затем проверьте результаты, выполнив соответствующие десятичные сложения:
| а) 10111012 и 11101112; | д) 378 и 758; | и) A16 и F16; |
| б) 1011,1012 и 101,0112; | е) 1658 и 378; | к) 1916 и C16; |
| в) 10112, 112 и 111,12; | ж) 7,58 и 14,68; | л) A,B16 и E,F16; |
| г) 10112 , 11,12 и 1112; | з) 68, 178 и 78; | м) E16, 916 и F16. |
4.18. В каких системах счисления выполнены следующие сложения? Найдите
основания каждой системы:
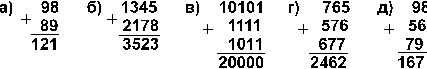
4.19. Найдите те подстановки десятичных цифр вместо букв, которые делают правильными выписанные результаты (разные цифры замещаются разными буквами):
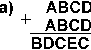
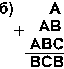
4.20. Вычтите:
| а) 1112 из 101002; | д) 158 из 208; | и) 1А16 из 3116; |
| б) 10,112 из 100,12; | е) 478 из 1028; | к) F9E16 из 2А3016; |
| в) 111,12 из 100102; | ж) 56,78 из 1018; | л) D,116 из B,9216; |
| г) 100012 из 1110,112; | з) 16,548 из 30,018; | м) ABC16 из 567816. |
4.21. Перемножьте числа, а затем проверьте результаты, выполнив
соответствующие десятичные умножения:
| а) 1011012 и 1012; | д) 378 и 48; |
| б) 1111012 и 11,012; | е) 168 и 78; |
| в) 1011,112 и 101,12; | ж) 7,58 и 1,68; |
| г) 1012 и 1111,0012; | з) 6,258 и 7,128. |
4.22. Разделите 100101102 на 10102 и проверьте результат, умножая делитель на частное.
4.23. Разделите 100110101002 на 11002 и затем выполните соответствующее десятичное и восьмеричное деление.
4.24. Вычислите значения выражений:
4.25. Расположите следующие числа в порядке возрастания:
4.26. Запишите уменьшающийся ряд чисел +3, +2, ..., –3 в однобайтовом формате:
4.27. Запишите числа в прямом коде (формат 1 байт):
а) 31; б) –63; в) 65; г) –128.
4.28. Запишите числа в обратном и дополнительном кодах (формат 1 байт):
а) –9; б) –15; в) –127; г) –128.
4.29. Найдите десятичные представления чисел, записанных в дополнительном коде:
а) 1 1111000; б) 1 0011011; в) 1 1101001; г) 1 0000000.
4.30. Найдите десятичные представления чисел, записанных в обратном коде:
а) 1 1101000; б) 1 0011111; в) 1 0101011; г) 1 0000000.
4.31. Выполните вычитания чисел путем сложения их обратных
(дополнительных) кодов в формате 1 байт. Укажите, в каких случаях имеет место
переполнение разрядной сетки:
| а) 9 – 2; | г) –20 – 10; | ж) –120 – 15; |
| б) 2 – 9; | д) 50 – 25; | з) –126 – 1; |
| в) –5 – 7; | е) 127 – 1; | и) –127 – 1. |